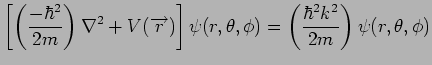 |
(9.1) |
Polazna tacka u daljim razmatranjima je Šredingerova
jednacina sa hamiltonijanom (4.14):
Ogranicicemo se na sferno simetricni potencijal:
![]() . Rešavacemo jednakost
(B.1) metodom separacije varijabli. U faktor prostoru
. Rešavacemo jednakost
(B.1) metodom separacije varijabli. U faktor prostoru
![]() dobijamo sferne harmonike
dobijamo sferne harmonike
![]() , a u radijalnom faktor prostoru
, a u radijalnom faktor prostoru
![]() preostaje
preostaje
Mnozeci dobijenu jednakost sa
![]() i koristeci se jednakošcu:
i koristeci se jednakošcu:
![]() , odmah sledi:
, odmah sledi:
gde je
![]() . Imajuci u vidu
da je naš problem rasejanja aksijalno simetrican ogranicicemo
razmatranje samo na aksialno simetricna rešenja.
To su rešenja koja ne zavise od
. Imajuci u vidu
da je naš problem rasejanja aksijalno simetrican ogranicicemo
razmatranje samo na aksialno simetricna rešenja.
To su rešenja koja ne zavise od ![]() , tj. ona za
koje je magnetni kvantni broj
, tj. ona za
koje je magnetni kvantni broj ![]() . Stanje rasejanja moramo razviti
po
. Stanje rasejanja moramo razviti
po ![]() , [41]:
, [41]:
uzimajuci da je funkcija
![]() jednaka, s tacnošcu do konstante, Legrende-ovom polinomu
jednaka, s tacnošcu do konstante, Legrende-ovom polinomu
![]() .
.
Kao što smo videli nama je ustvari potrebna samo
asimptotska forma od
![]() . Izracunacemo asimptotsku
formu pojedinih
. Izracunacemo asimptotsku
formu pojedinih ![]() . U asimptotskom regionu
(B.3) se svodi na
. U asimptotskom regionu
(B.3) se svodi na
Opšte rešenje jednacine (B.5) glasi
![]() ili ekvivalentno
ili ekvivalentno
![]() . Ispostavlja se da je pogodno
staviti
. Ispostavlja se da je pogodno
staviti
![]() ,
,
![]() . Tako da ce izraz za
. Tako da ce izraz za
![]() biti:
biti:
Ugao
![]() predstavlja razliku u fazi izmedju
asimptotskog izraza stvarne radijalne funkcije
predstavlja razliku u fazi izmedju
asimptotskog izraza stvarne radijalne funkcije ![]() i radijalne
funkcije
i radijalne
funkcije ![]() slobodnog kretanja
slobodnog kretanja
![]() i zato se velicina
i zato se velicina
![]() naziva fazni pomeraj
naziva fazni pomeraj ![]() parcijalnog talasa.
parcijalnog talasa.
Potrebno je da razvijemo ravan talas po sfernim talasima
gde je
![]() sferna Besselova funkcija. Asimptotska
forma od sferne Besselove funkcije glasi
sferna Besselova funkcija. Asimptotska
forma od sferne Besselove funkcije glasi
![]() .
.
Sad mozemo asimptotsku formu od
![]() izjednaciti sa asimptotskom formom
izjednaciti sa asimptotskom formom
![]() (4.15)
(4.15)
Posle sredjivanja izraza tj. jednakosti (B.8) dobijamo izraz za amplitudu rasejanja ![]()
Prema tome pošto je
![]() , a
, a
![]() ako
ako
![]() ne zavisi od
ne zavisi od ![]() , imamo
, imamo
Posto su Legendre-ovi polinomi ortogonalni
totalni presek za rasejanje, definisan sa
![]() moze se napisati u
obliku
moze se napisati u
obliku
a transportni presek za elasticno rasejanje definisan je sa
U (B.12), (B.13) se pojavljuju
preseci ![]() ,
,
![]()
u kojima imamo fazne pomake
![]() kao otvoren
tj. nepoznat broj. Dejstvo potencijala
kao otvoren
tj. nepoznat broj. Dejstvo potencijala ![]() interakcije
interakcije ![]() ispoljava se u faznim pomacima.
ispoljava se u faznim pomacima.